

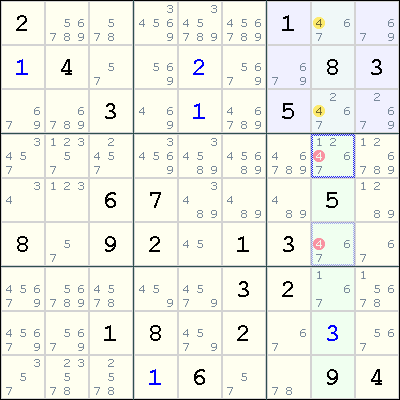
> putStrLn $ showGridWithPossibilities grid 1 4 2 5 4 7 8 3 1 9 3 4 2 5 1 8 6 We can write a few functions to clean it up: The output is a bit unreadable but correct. > Just grid = readGrid ".1.4.2.5.4.7.8.3.1.9.3.4.2.5.1.8.6." > mapM_ print grid ,Possible ,Possible ,Possible ,Possible ,Possible ,Possible ,Fixed 1,Possible ] ,Possible ,Possible ,Possible ,Possible ,Possible ,Possible ,Possible ] ,Fixed 2,Possible ,Possible ,Possible ,Possible ,Possible ,Possible ,Possible ] ,Possible ,Possible ,Possible ,Fixed 5,Possible ,Fixed 4,Possible ,Fixed 7] ,Possible ,Fixed 8,Possible ,Possible ,Possible ,Fixed 3,Possible ,Possible ] ,Possible ,Fixed 1,Possible ,Fixed 9,Possible ,Possible ,Possible ,Possible ] ,Possible ,Fixed 4,Possible ,Possible ,Fixed 2,Possible ,Possible ] ,Fixed 5,Possible ,Fixed 1,Possible ,Possible ,Possible ,Possible ,Possible ] ,Possible ,Possible ,Fixed 8,Possible ,Fixed 6,Possible ,Possible ,Possible ] For example, a grid showing the possibilities of all non-filled cells for the sample puzzle above: Each cell contains either a single digit or has a set of possible digits.Given these constraints, we can devise a simple algorithm to solve Sudoku: For example, if a cell contains 1 then no other cell in that cell’s row, column or sub-grid can contain 1. Digits in the pre-filled cells impose constraints on the rows, columns, and sub-grids they are part of. Each of the nine 3x3 sub-grids must have all the digits, from 1 to 9.Įach cell in the grid is member of one row, one column and one sub-grid (called block in general).Each of the nine columns must have all the digits, from 1 to 9.Each of the nine rows must have all the digits, from 1 to 9.We are given a partially filled grid which we have to fill completely such that each of the following constraints are satisfied: Solving Sudoku is a constraint satisfaction problem. Fast Sudoku Solver in Haskell #3: Picking the Right Data Structures.Fast Sudoku Solver in Haskell #2: A 200x Faster Solution.Fast Sudoku Solver in Haskell #1: A Simple Solution.This is the first post in a series of posts: We’ll focus on both implementing the solution and making it efficient, step-by-step, starting with a slow but simple solution in this post 1. The aim of this series of posts is to write a fast Sudoku solver in Haskell. It is a good choice to solve Sudoku given the problem’s combinatorial nature. Haskell is a purely functional programming language. Some of the cells of the grid come pre-filled and the player has to fill the rest. It consists of a 9x9 grid which is to be filled with digits from 1 to 9. Tags: programming puzzles haskell nilenso.It’s also called the brute force algorithm way to solve the sudoku puzzle.Fast Sudoku Solver in Haskell #1: A Simple Solution | About Posts Notes Photos Readings Now Fast Sudoku Solver in Haskell #1: A Simple Solution We use this principle of backtracking to implement the sudoku algorithm. Backtracking means switching back to the previous step as soon as we determine that our current solution cannot be continued into a complete one.

We’ll use the backtracking method to create our sudoku solver in Python. As our assumption was wrong, we discard the assigned num and then we go for the next assumption with a different num value.Later we check for the next possibility with the next column. After checking if it is a safe place, we move to the next column and then assign the num in the current (row, col) position of the grid.Further now we see if the current position of the grid has a value greater than 0, then we iterate for the next column.Next, we will check if the column value becomes 9 then we move to the next row and column.Then we will check if we have reached the 8th row and 9th column and return true for stopping further backtracking.If we find the same num in the same row or same column or in the specific 3*3 matrix, ‘false’ will be returned.Later it will assign num to the row and col.Then we assign the utility function (puzzle) to print the grid.In this method for solving the sudoku puzzle, first, we assign the size of the 2D matrix to a variable M (M*M).Steps to solve the Sudoku Puzzle in Python The lesser the clues, the higher the chances of multiple solutions. It is unknown whether or not there exists a well-formed puzzle with only 16 clues. Well-formed Sudoku with 17 symbols exists. Another challenging research problem is to determine how few boxes need to be filled for a Sudoku puzzle to be well-formed. A Sudoku puzzle is believed to be well-formed if it has a unique solution. The Sudoku puzzles which are published for entertainment have unique solutions.


 0 kommentar(er)
0 kommentar(er)
